上一篇讲解了《增广拉格朗日方法求解带约束优化问题》，套路是外层ALM和内层ilqr进行无约束优化。内层可以用ilqr做无约束优化问题求解，那么可以用其他方法求解吗？答案是可以的，如lbfgs也可以用于无约束优化问题。

恰好最近看到一篇论文，用的是ALM(增广拉格朗日法)+LBFGS(拟牛顿法)，下边让我们来看一下。

让人兴奋的一点是，论文里提到：

一个统一的轨迹可以同时处理前进和后退运动，而不是由规划前端指定

这里无需前端提供换挡点，也就是无需混合a星来提供初始解。那这不就是直接革了hybrid a star的命了嘛。让我们来仔细的学习这篇文章，看一看到底是怎么回事。后续要结合开源代码看一下实际效果。

这篇论文提出了一个面向差速驱动机器人（包括轮式与履带式）的统一轨迹优化框架。作者基于瞬时旋转中心（ICR）建立通用运动学模型，并用运动状态表示法（在姿态与弧长空间构造多段多项式轨迹）使轨迹天然满足连续性和运动学约束。在约束处理上，论文创新性地结合了惩罚函数（处理速度、加速度、安全等不等式约束）与增广拉格朗日方法（仅处理终点位置等式约束），既保证了精度又提高了数值稳定性。

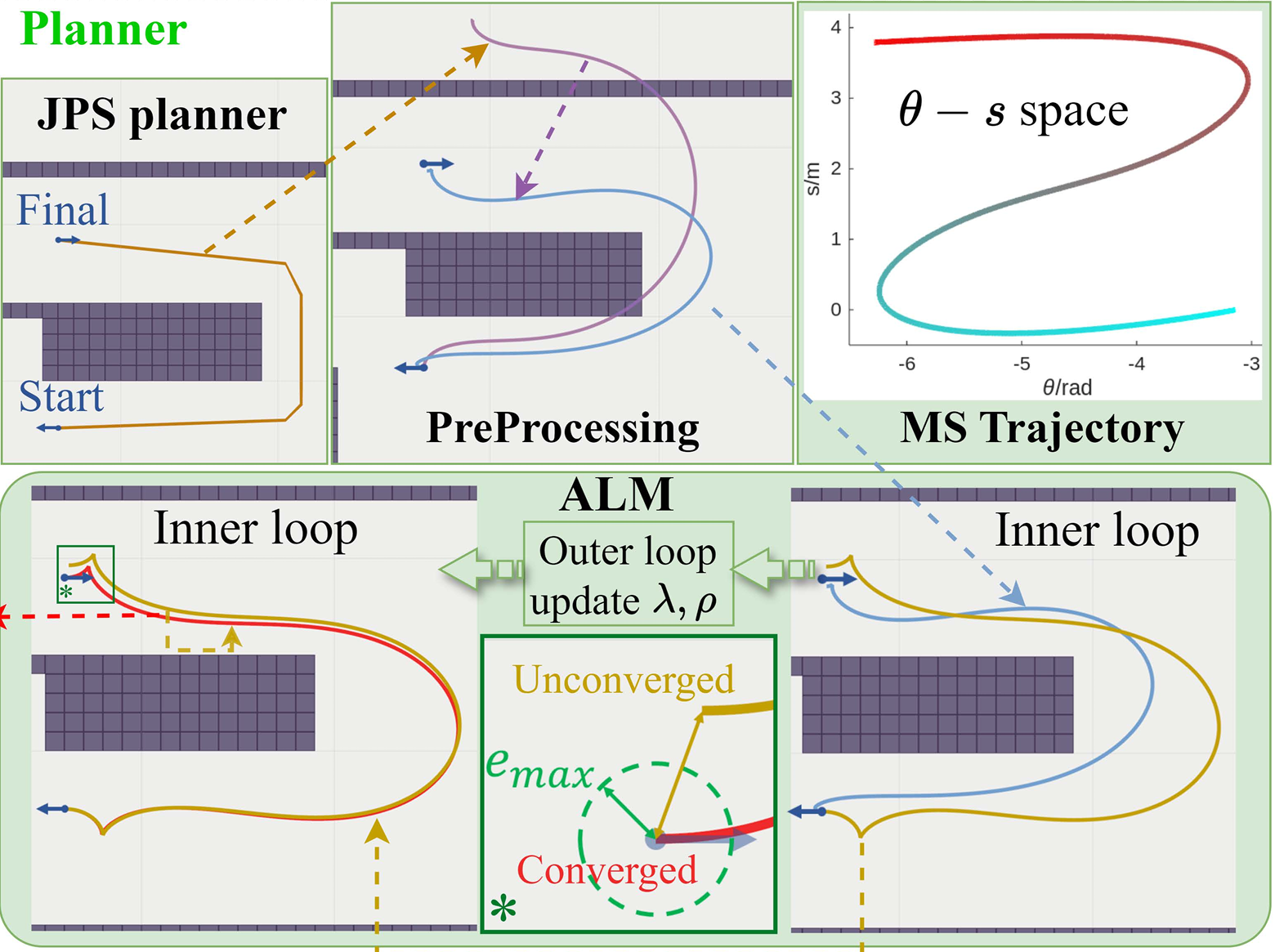
算法的示意图如下，非常有意思的研究，其中的一些处理技巧，可以在自己的工作中灵活应用，建议收藏和点赞，有空再看！

1.轨迹表示

在本节中，我们重点介绍一种基于运动状态多项式参数化的全新轨迹表示方法。

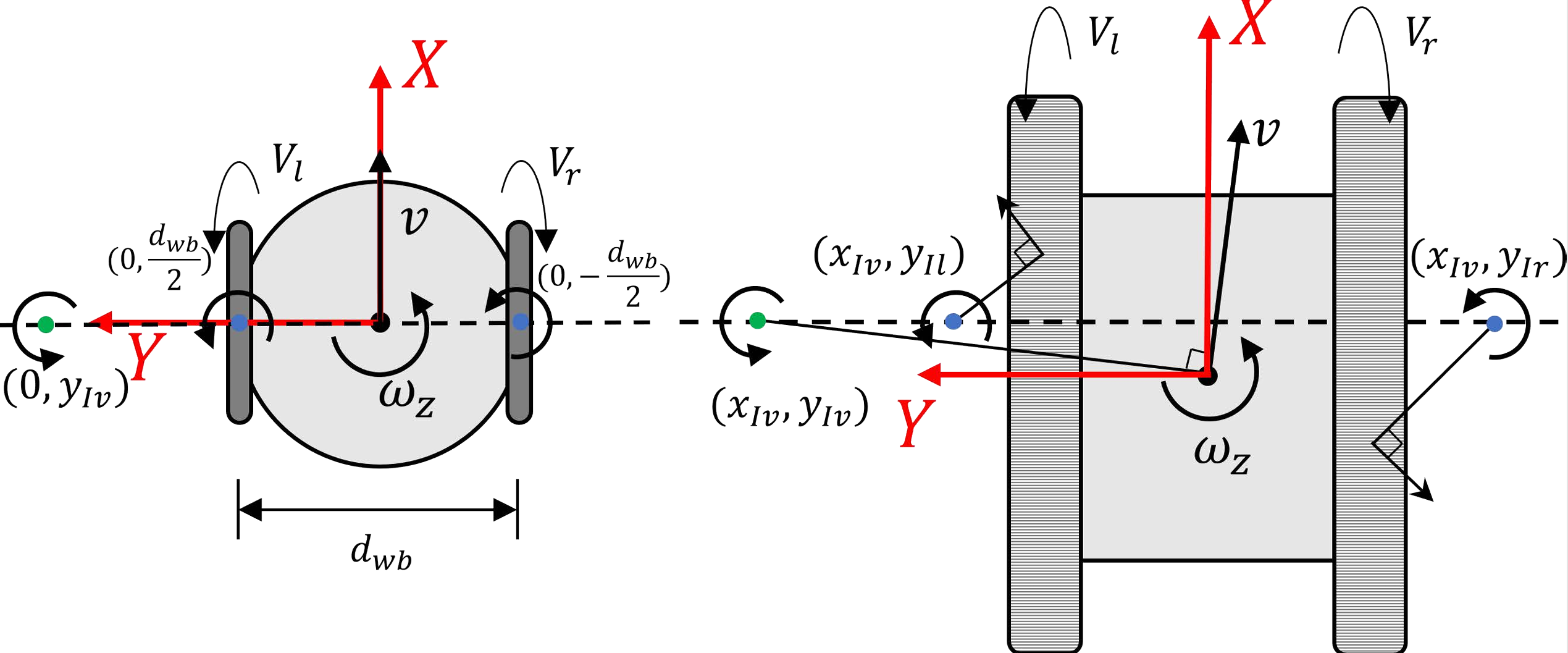
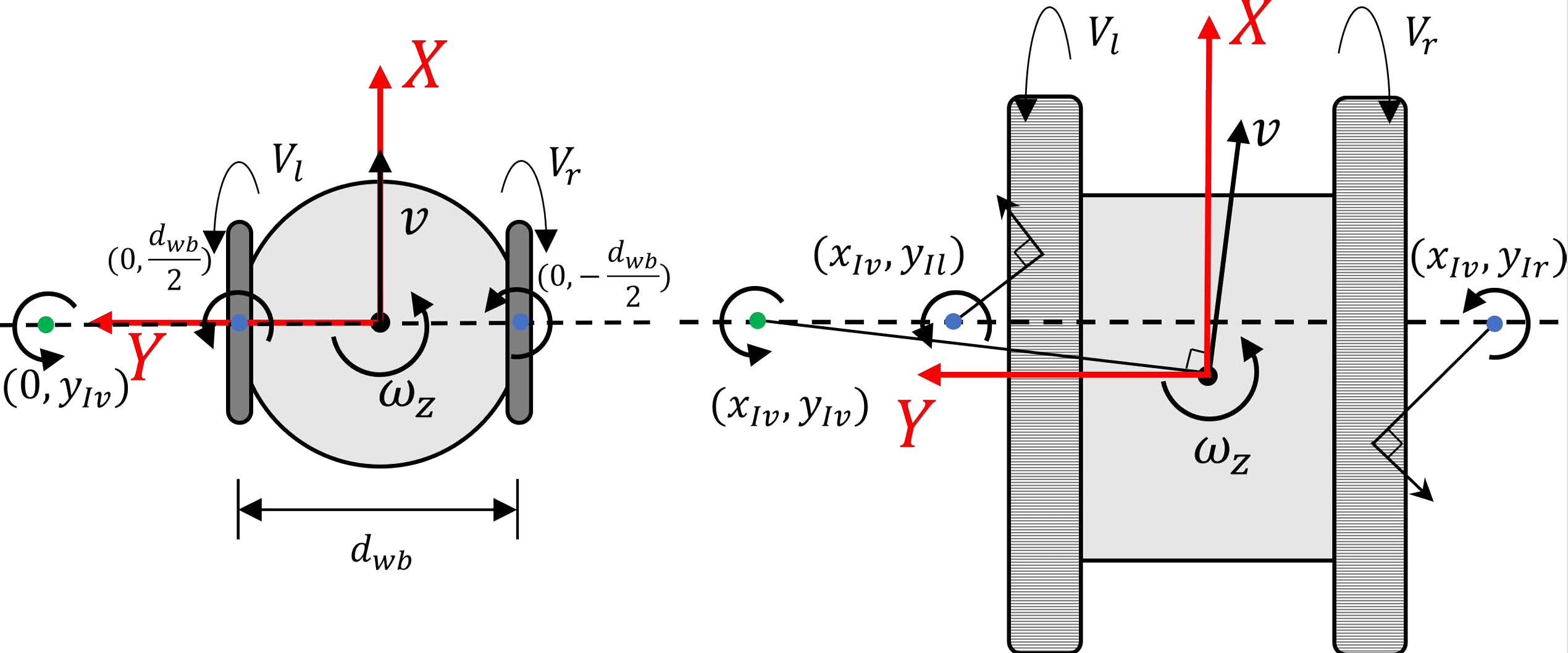
A. 差分驱动机器人的运动学模型

• 绿色点：表示机器人机体的瞬时旋转中心（ICR of body）。
• 蓝色点：表示左右驱动轮或履带与地面的接触点的 ICR。
• 机体坐标系：
  • 原点在几何中心（两轮中点或履带几何中心）。
  • x 轴：与机器人前进方向对齐。
  • y 轴：与车体横向方向对齐。

我们采用 瞬时旋转中心（Instantaneous Centers of Rotation, ICRs） [1] 来描述差分驱动机器人的运动，如图 3 所示。通过引入 ICR，可以方便地将机器人几何中心定义为机体坐标系的原点，并使 x 轴与机器人朝向保持一致。此时，机器人的瞬时平移与旋转速度可以表示为：

• $\omega$：机器人机体的角速度（绕 z 轴）。
• $V_r, V_l$：右轮（或右履带）、左轮（或左履带）的线速度。
• $y_{Il}, y_{Ir}$：左右驱动轮（或履带）的瞬时旋转中心在机体坐标系 y 轴上的位置。
• 含义：角速度由左右轮速差决定，并与轮距（$y_{Il}-y_{Ir}$）成反比。

• $v_x$：机体坐标系下的纵向速度（沿 x 轴）。
• $\frac{V_r + V_l}{2}$：左右轮速度的平均值，表示机器人前进/后退的主体速度。
• $\frac{V_r - V_l}{y_{Il} - y_{Ir}}$：对应角速度 $\omega$。
• $\frac{y_{Il} + y_{Ir}}{2}$：左右轮 y 坐标的平均值。
• 含义：纵向速度不仅取决于左右轮速度的平均值，还受到旋转引起的几何中心偏移的影响。

• $v_y$：机体坐标系下的横向速度（沿 y 轴）。
  • 对于标准两轮差速车（SDD），$v_y = 0$，因为几何中心始终在两轮连线的中点，不存在横向滑移。
  • 对于滑移转向或履带机器人（SKDD/TDD），由于接触点与几何中心存在偏差，$v_y \neq 0$。
• $x_{Iv}$：机体 ICR 的 x 坐标。
• $x_{Iv} = -\omega x_{Iv}$：表明横向速度与旋转半径和角速度有关。

对于 SDD 机器人，其车轮的 ICR 位于与地面的接触点，满足 $y_{Il} = -y_{Ir} = d_{wb}/2$，其中 $d_{wb}$ 为轮距，且不存在横向滑移（$x_{Iv} = 0$）。机体坐标系的原点位于两驱动轮的中点。为了保证方法的普适性，我们在不同驱动机制下均采用式 (1)–(3) 进行轨迹计算。

B. 运动状态轨迹

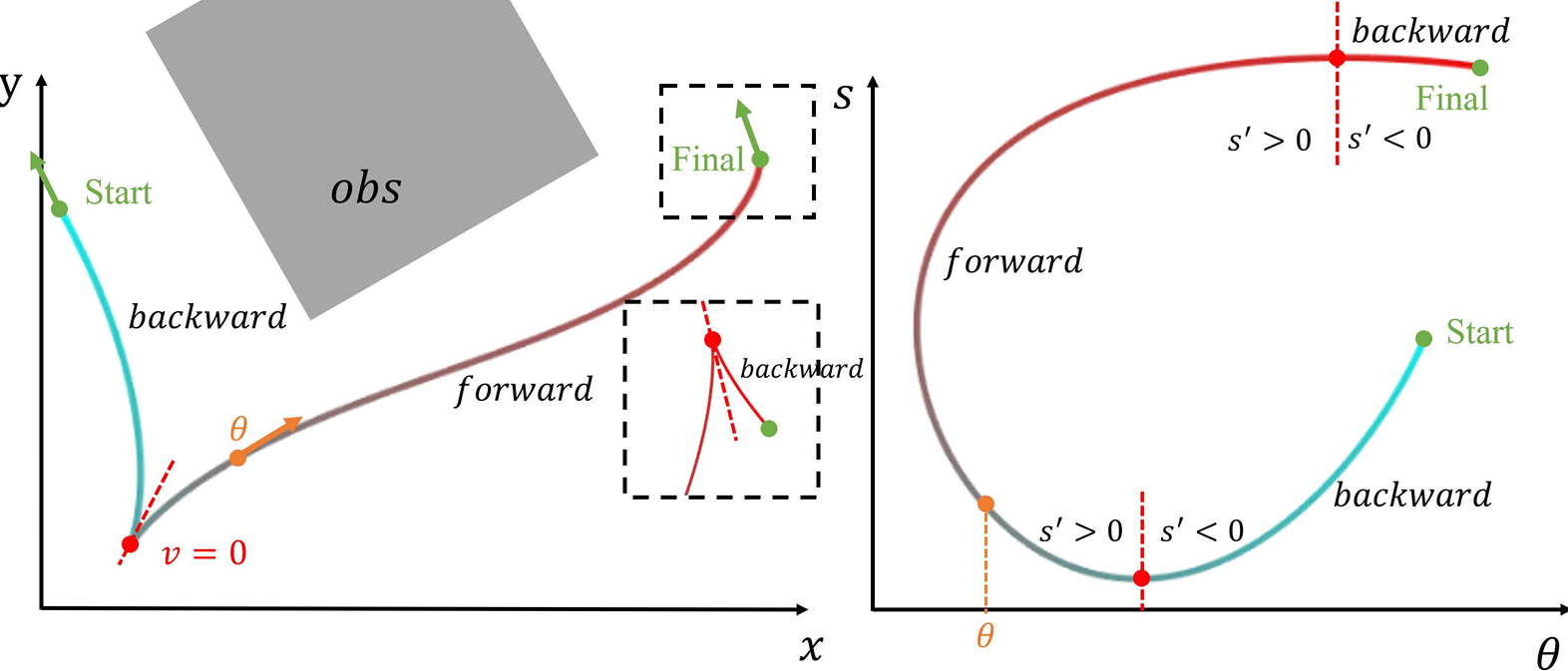
在移动机器人规划中，常见的做法是直接在平面坐标 $(x,y)$ 上规划轨迹。但这样对差速车、履带车等 非完整约束 的机器人来说会遇到几个问题：

• 一旦轨迹包含前进/后退切换，轨迹在 $(x,y)$ 空间会出现奇异点（不可导、跳变）。
• 控制器在跟踪这些轨迹时会不稳定。

解决思路：换一种表达方式。我们不直接画 $(x,y)$ 曲线，而是先在 朝向角 $\theta(t)$ 和 前进弧长 $s(t)$ 空间画轨迹，这样轨迹天然光滑、连续，再通过积分还原出 $(x,y)$。

这种方法被称为 运动状态轨迹 (Motion State Trajectory, MS Trajectory)。

(1) 如何表示一条轨迹？

我们把轨迹分成多段，每一段的朝向角和前进弧长，都用 时间多项式 来表示：

这里：

• $\theta(t)$：表示机器人朝向角随时间的变化。
• $s(t)$：表示机器人在前进方向上的累计弧长。
• $\beta(t) = [1, t, t^2, \dots, t^{2h-1}]^T$：多项式基底向量。
• $c_{\theta}, c_{s}$：系数向量，决定曲线形状。

重要导数：

• $\dot s(t) = v_x(t)$：前向速度。
• $\dot \theta(t) = \omega(t)$：角速度。 也就是说，轨迹一旦在 $(\theta, s)$ 空间被描述，就自动包含了速度和角速度信息。

(2) 如何还原平面位置？

虽然轨迹在 $(\theta,s)$ 空间更好，但最终我们还是要得到 $(x,y)$ 以便检查避障和到达目标点。 机器人在平面中的坐标由积分得到：

解释：

• $(x_0,y_0)$：起点坐标。
• $\dot s \cos\theta, \dot s \sin\theta$：表示正常前进的位移分量。
• $x_{Iv}$：车体几何中心和瞬时旋转中心 (ICR) 的偏移量，反映了横滑效应。
• 当机器人转弯时，如果有横滑，就会额外产生位移，这由 $x_{Iv}\dot\theta$ 项体现。

(3) 如何计算积分？

直接算上面的积分很难，所以引入 Simpson 公式 来近似：

通俗的解释：

• 在区间的左端点、中点、右端点各取一个采样值。
• 用权重 $1:4:1$ 加权平均，就能高精度近似积分。

这种方法既快又准，非常适合轨迹优化中实时计算。

(4) 整条轨迹的数值积分

1. 先分段：整条轨迹切成 $M$ 段，方便用多项式“拼”出复杂曲线（像用多段样条曲线）。
2. 再分小区间：每段再切成 $n$ 个小区间。积分就是“面积求和”，我们要算 $$x\text{ 位移}=\int \big[\dot s\cos\theta + x_{Iv}\dot\theta\sin\theta\big]\,dt.$$
3. 每个小区间只看三个点：左端、中点、右端，函数值按权重 $1:4:1$ 相加，再乘上小区间长度的 $\frac{1}{6}$，就得到这一小块的“面积近似”。
4. 把所有小块加起来：得到该段的近似位移 $x_i$；最后把所有段的 $x_i$ 累加，再加起点 $x_0$，得到整条轨迹末端的 $x$。
5. 为什么可行：Simpson 对平滑函数很准，且误差随 $n^4$ 衰减（在式(9)里给出误差上界），所以用少量采样点就能得到高精度的积分，计算量小，适合优化与实时。

一条轨迹通常分为 $M$ 段，每段再分成 $n$ 个小区间。对每个小区间应用 Simpson 公式，就能近似整段积分。 整体：

每段的复合 Simpson 近似：

每个小区间的 integrand（被积函数在采样点的值）：

采样时刻（每段时间网格）：

• $M$：分段数。整条轨迹被分成 $M$ 段，每段单独用多项式描述，便于形状控制和数值稳定。
• $i \in \{1,\dots,M\}$：段索引，指向第 $i$ 段。
• $T_i$：第 $i$ 段的持续时间（长度）。不同段可以长短不同。
• $n$：每段再切分的小区间数（复合 Simpson 的“复合”来自这里）。每个小区间里用一次 Simpson 三点公式。
• $j \in \{1,\dots,n\}$：第 $i$ 段内部的小区间索引。
• $l \in \{0,1,2\}$：小区间内三类采样点的编号，分别代表左端点($l=0$)、中点($l=1$)、右端点($l=2$)。
• $T_i^{\,j,l}=\dfrac{2(j-1)+l}{2n}\,T_i$：第 $i$ 段第 $j$ 个小区间内第 $l$ 个采样点的时间位置。
  • 等价理解：把第 $i$ 段的时间 $[0,T_i]$ 均匀切成 $2n$ 段，节点为 $t_{i,k}=k\cdot\frac{T_i}{2n}$；则
    • 左端点 $T_i^{\,j,0}=t_{i,2j-2}$，
    • 中点 $T_i^{\,j,1}=t_{i,2j-1}$，
    • 右端点 $T_i^{\,j,2}=t_{i,2j}$。
• $x_0$：起点的 x 坐标。
• $\tilde{x}_f$：用数值近似得到的终点 x 坐标（或某一时刻的累计 x 位移），这里是“近似”的意思，用 $\tilde{(\cdot)}$ 表示。
• $x_i(c_i,T_i)$：第 $i$ 段对 x 位移的近似贡献。依赖于该段的多项式系数 $c_i$（包括 $\theta$ 和 $s$ 两组）以及段时长 $T_i$。
• $\hat{x}_i^{\,j,l}$：被积函数 $f(t)$ 在采样时刻 $T_i^{\,j,l}$ 的数值（就是“瞬时 x 方向位移密度”）： $$\hat{x}_i^{\,j,l} = \dot s\!\big(T_i^{\,j,l}\big)\cos\!\big(\theta_i(T_i^{\,j,l})\big) + x_{Iv}\,\dot\theta_i(T_i^{\,j,l})\sin\!\big(\theta_i(T_i^{\,j,l})\big).$$
• $\dot s(t)$：前向线速度（车体坐标系 x 轴方向的速度），也就是 $s(t)$ 对时间的导数。
• $\theta_i(t)$、$\dot\theta_i(t)$：朝向角及其角速度（第 $i$ 段的多项式及其导数求得）。
• $x_{Iv}$：ICR 偏移/横滑参数。若平台存在横滑或几何中心不在瞬时旋转中心上，这一项就不为 0，它会让角速度对 x 方向位移也产生贡献。

(5) 为什么 $(\theta,s)$ 空间更好？

如果直接在 $(x,y)$ 空间表示轨迹，当机器人前进一段、再倒车时，曲线会出现奇异点（轨迹不再光滑）。换到 $(\theta,s)$ 空间后：

• 前进/后退只需要改变 $s(t)$ 的正负。
• 整条轨迹依旧是光滑曲线。 这也是论文中图4所展示的核心对比：
• 红点：在 $(x,y)$ 空间出现的奇异点。
• 平滑曲线：在 $(\theta,s)$ 空间的自然表示。

2. 轨迹优化问题

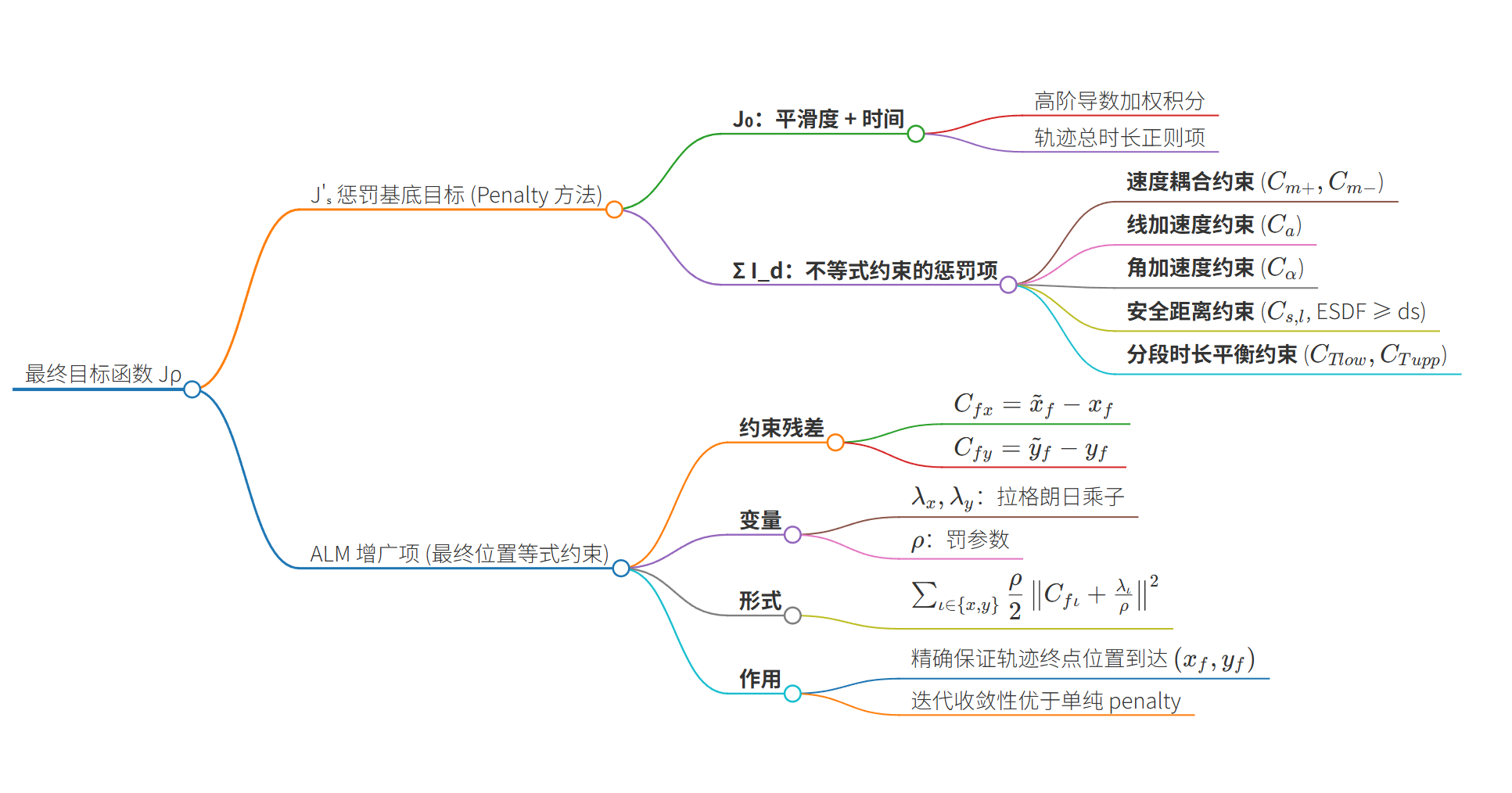
接下来让我们基于 MS 轨迹表示 构建轨迹优化问题。 先看一下最终的目标函数：

将目标展开是这样的：

下边我们开始逐步讲解优化问题如何得到的。

A. 轨迹优化问题的形式化

基于前面提出的新型轨迹表示，我们构造优化问题如下：

• $c$：将所有分段多项式系数纵向拼接后的系数向量（见式(11)）。
• $T=[T_1,\dots,T_M]^T$：各段时长。
• $\sigma^{(h)}(t)=[\theta^{(h)}(t),\; s^{(h)}(t)]^T$：对 $\theta$ 与 $s$ 的 第 $h$ 阶导（若 $h=3$ 就是 jerk）。
• $W\in\mathbb{R}^{2\times 2}$：对角权重矩阵（分配角/弧长方向的平滑权重）。
• $\epsilon_T>0$：时间正则权重（鼓励短时长）。
• 含义：让高阶导数小（轨迹更平滑），同时抑制时长过大。

约束条件为：

(1) 初始条件：

这里就相当于在笛卡尔系时，我们指定起点的位置，加速度等起始条件。这里用的是朝向$\theta$ 和弧长$s$.

• $\sigma^{[h-1]}(t)$：从 0 阶到 $h\!-\!1$ 阶导数组成的列向量：
  $\sigma^{[h-1]}=[\theta,\dot\theta,\dots,\theta^{(h-1)},\; s,\dot s,\dots,s^{(h-1)}]^T$。
• $\sigma^{[h-1]}_0$：起点处上述各量的给定值（其中 $s_0\!=\!0$）。

(2) 终止条件：

类比在笛卡尔系规划时，我们指定的终止条件如终点的位置，速度，加速度，曲率等。这里用的是角度，角速度，角加速度，以及弧长，纵向速度，纵向加速度。

• $\theta^{[h-1]}$：$\theta$ 的 0～$h\!-\!1$ 阶导数组合。
• $s^{[h-1]/[0]}$：从 1 阶到 $h\!-\!1$ 阶的导数组合（不含 0 阶位置）。
• 含义：最终角度及其导数被固定；$s$ 的速度/加速度等被固定，但 $s(T_s)$（终止弧长）不固定，这为后续自动确定“行驶距离 / 前后切换”留下自由度。

(3) 最终位置：

• $(\tilde{x}_f,\tilde{y}_f)$：由 数值积分（Simpson，见前文(8)）从 $\theta,s$ 推到笛卡尔得到的近似终点。
• $(x_f,y_f)$：目标终点。
• 含义：轨迹的积分终点要落在目标点（后文(22)–(25)用增广拉格朗日迭代逼近）。

(4) 分段连续性：

整条轨迹被划分为 $M$ 段，每一段由一个 $(2h-1)$ 阶的二维多项式表示。因此，每段之间需要一个等式约束。这里就类似于分段贝塞尔曲线了。

• 要求相邻段在 0～$h\!-\!1$ 阶全部连续（位置、速度、加速度…）。

(5) 时间：

轨迹执行时间许越小越好，因此这里把时间总和也作为代价。

• 含义：时长为正且可分配。

(6) 约束集合：

• $C_d(\cdot)$：具体约束（如速度/加速度界、运动学界、安全距离等）。

(7) 采用ΣMINCO轨迹类来表示轨迹

为了解决该优化问题，我们采用 ΣMINCO [25] 轨迹类 来表示轨迹，并将优化变量进行变换。通过 ΣMINCO，可以把多项式系数 $c$ 唯一地表示为：

• $c$：所有分段多项式系数拼接向量（优化变量之一）。
• $K(T)\in\mathbb{R}^{2Mh\times 2Mh}$：由时长 $T$ 决定的可逆带状矩阵（参考[25]），把“边界/拼接点状态”与“系数”一一映射。
• $\sigma'_{i,0}$：第 $i$ 段末端状态（中间点）的某种拼接形式；其后的 “$0$” 表示按 ΣMINCO 约定在向量中补零以成固定维度。

然而，目标终点一般是用笛卡尔坐标 $(x_f,y_f)$ 表示，而不是终止弧长 $s_f$。 因此式 (11) 中的最终状态 $\sigma^{[h-1]}_f$ 并不是固定的，特别是 $s_f$ 并不预先给定，而应作为优化变量的一部分。 这意味着轨迹的行驶距离在优化前是未知的。 因此需要考虑代价函数 $J$ 对 $s_f$ 的梯度。假设 $\frac{\partial J}{\partial c}$ 已经通过 ΣMINCO 的方法求得，则有：

其中 $e_i$ 是单位矩阵 $I_{2Mh}$ 的第 $i$ 列。
本文选择 $h=3$，以最小化线性与角加加速度（jerk），从而生成平滑轨迹。

B. 不等式约束与梯度传播

对于目标函数 (10a)，其梯度可以直接计算。
由于时间变量 $T_i$ 要求严格为正 (10f)，我们将 $T_i \in \mathbb{R}^+$ 转换为无约束变量 $\tau_i \in \mathbb{R}$，通过如下光滑双射：

对于不等式约束 (10g)，我们采用惩罚方法，结合一阶松弛函数 $L_1(\cdot)$ [26]。
通过对轨迹上的采样点进行约束，可以确保整个轨迹满足约束：

• $C_d^{i,j}(c,T)$：在 第 $i$ 段、第 $j$ 个采样点 上的约束值。
• $c_i$：第 $i$ 段的多项式系数。
• $\beta(\cdot)$：基函数。$\beta^{(h-1)}$ 是其高阶导数。
• $x_{i,j}, y_{i,j}$：采样点的位置信息（通过数值积分得到，不是直接由多项式表达的）。

罚项构造：

• $\zeta_d$：约束 $d$ 的权重（控制罚项的力度）。
• $(\nu_0, \dots, \nu_n) = (0.5, 1, \dots, 1, 0.5)$：梯形积分的系数。
  • 用它可以把区间积分近似为采样点加权求和。
• $L_1(\cdot)$：一阶松弛罚函数（smooth penalty function）。
  • 当 $C_d \le 0$（满足约束）时，$L_1(C_d) \approx 0$。
  • 当 $C_d > 0$（违反约束）时，$L_1(C_d) > 0$，随违反程度增加。
• $I_d(c,T)$：整个轨迹在约束 $d$ 下的总罚项。

其中，$\varsigma_d$ 是约束 $d$ 的权重，
$(\nu_0,\dots,\nu_n) = (0.5,1,\dots,1,0.5)$ 为梯形积分系数。
$n$ 与积分区间数保持一致，避免过计算。

于是，优化问题可以重新写为：

• $J_0$：原始目标（平滑 + 时间）。
• $I_d$：所有约束的罚项。
• 优化变量：
  • $w_{\sigma'}$：轨迹中间状态，
  • $\tau$：时间变量的无约束形式，
  • $s_f$：末端弧长。

梯度为什么重要？

公式（15）是一个 无约束非线性优化问题，本质上靠数值迭代解。在本文中:

• 等式约束（终点、段间连续性）：用 PHR-ALM 增广拉格朗日，逐步修正，确保严格满足。
• 不等式约束（避障、速度等）：用 罚函数法，把它们变成目标函数的附加项。 处理完之后，优化问题就变成了一个 光滑的无约束优化问题。最后的无约束优化问题是用 L-BFGS（Limited-memory BFGS）来解的。因为 L-BFGS 是一个 梯度型方法,所以我们要准确计算相应的梯度。涉及到的梯度如下表：

下表开始讨论梯度的计算公式。

(1) 约束对系数 $c$ 的梯度

• $C_d$：某个不等式约束函数。
• $c$：多项式系数向量。
• $\sigma^{(h)}$：状态的 $h$ 阶导数。
• $x,y$：位置信息（通过积分得到）。

通过链式法则，把约束对 $c$ 的梯度拆成三部分：

1. 对状态的直接依赖；
2. 对 $x$ 的间接依赖；
3. 对 $y$ 的间接依赖。

(2) 约束对时间 $T$ 的梯度

类似 (16)，只不过这里是约束对时间 $T$ 的导数。
因为 $T$ 会影响采样点位置和积分结果，所以必须单独考虑。

(3) 罚项 $I_d$ 对系数 $c$ 的梯度

• $\zeta_d$：约束权重。
• $\nu_j$：梯形积分权重 $(0.5, 1, \dots, 1, 0.5)$。
• $L_1(\cdot)$：松弛罚函数。

罚项对 $c$ 的梯度就是所有采样点梯度的加权和。

(4) 罚项 $I_d$ 对时间 $T$ 的梯度

• $e_i$：单位向量，确保只作用在对应的 $T_i$ 上。

罚项对 $T$ 的梯度有两部分：

1. 直接来自 $L_1(C_d)$；
2. 来自 $C_d$ 对 $T$ 的依赖。

(5) $x_{i,j}$ 对系数 $c$ 的梯度

• $x_{i,j}$：第 $i$ 段第 $j$ 个采样点的 $x$ 坐标。
• $c_m$：第 $m$ 段的多项式系数。
• $\Gamma_{m,k} = \hat{x}^{k,0} + 4\hat{x}^{k,1} + \hat{x}^{k,2}$：Simpson 加权和。
• $g^x_{i,j}$：约束函数对 $x_{i,j}$ 的敏感度。

$x_{i,j}$ 来自积分，所以它不仅依赖本段，还依赖所有前面段的系数。

(6) $x_{i,j}$ 对时间 $T$ 的梯度

与 (20) 类似，不过这里是 $x_{i,j}$ 对时间的梯度。 它表明 $x_{i,j}$ 的值会受前面所有段的时间分配影响。

C. 终点位置约束

与基于微分平坦性的轨迹不同，MS 轨迹的最终位置是通过积分近似计算得到的，因此可能与期望目标 $(x_f,y_f)$ 存在偏差。
为减少这种误差，需要专门引入终点位置约束。

以 $x$ 轴为例：

通常允许存在最大误差 $e_{\max}$。
虽然可以通过增大惩罚权重来提升精度，但这可能会改变轨迹拓扑，或导致收敛速度下降。
如果仅使用惩罚函数方法，优化结果可能达不到精度要求。

因此，作者采用 Powell-Hestenes-Rockafellar 增广拉格朗日方法 (PHR-ALM) 来迭代减少误差。
定义新的目标函数：

其中，$\lambda$ 为对偶变量，$\rho>0$ 为增广项权重。

更新方式如下：

其中 $\varrho>0$ 确保 $\rho^k$ 单调递增，$\rho_{\max}$ 用于避免过大。
优化问题由 L-BFGS求解，迭代执行式 (24)，直到满足：

即保证最终位置误差在容许范围内。

公式 (23) 是本文中最终的轨迹优化目标函数，它采用 Powell-Hestenes-Rockafellar 增广拉格朗日方法 (PHR-ALM) 来处理轨迹的最终位置约束。

该公式将需要精确满足的等式约束（最终位置）与所有通过惩罚函数方法处理的不等式约束统一在一个迭代可解的增广目标函数中。

统一约束的机制

公式 (23) 体现了优化框架对不同类型约束的分层处理策略：

1. 内层惩罚 ($J'_s$)： 所有的不等式约束（如耦合速度、加速度、安全距离等）都通过惩罚函数 $I_d$ 转化为目标函数的一部分，确保轨迹在优化过程中具备可行性和安全性。
2. 外层增广 ($J_\rho$)： 对于要求高精度的等式约束（即最终位置 $x_f, y_f$），则使用更强大的 ALM 框架。ALM 在迭代中不断优化轨迹参数 $w_{\sigma}', \tau, s_f$，使得包含所有惩罚项的 $J'_s$ 最小化，同时严格满足最终位置约束。这种方法避免了在处理等式约束时简单惩罚函数可能导致的拓扑改变或收敛速度慢的问题。

附件：问题列表

Q1.为什么要用$y_{Il}，y_{Ir}$ ？

这里对于标准的二轮差分底盘，没有横向滑移，$y_{Il}-y_{Ir}=d_{wb}$，即两轮之间的距离，但如果是履带式的，当机器人转弯时，几何中心不再严格处于左右接触点连线的中点，而是发生偏移，$y_{Il}-y_{Ir} \neq d_{wb}$。- $y_{Il}, y_{Ir}$ 在公式 (1)(2)(3) 里不是单纯几何常量，而是 动力学/运动学模型中的等效参数。这就是为什么论文里要用 EKF 来在线估计 ICR 参数。)

Q2. iLQR / MPC 的线性化 vs Simpson 数值积分

(1) iLQR 的线性化

• 对象：非线性动力学 $x_{t+1} = f(x_t,u_t)$
• 方法：在参考轨迹附近做泰勒展开，一阶近似 $$\delta x_{t+1} \approx A_t \delta x_t + B_t \delta u_t$$
• 目的：把非线性 OCP 转化为 LQR 子问题，通过迭代求得全局近似最优解。
• 特点：迭代优化，全局一致性，计算量大。

(2) MPC 的逐步线性化

• 对象：非线性动力学
• 方法：在每个滚动时域的当前状态处线性化，只解一次优化问题。
• 目的：得到实时可用的控制输入，保证 MPC 能在强约束下运行。
• 特点：不迭代，每步线性化一次，实时性好但最优性弱。

(3) Simpson 数值积分

• 对象：积分算子，例如轨迹坐标转换 $$x(t)=\int_0^t [\dot{s}(\tau)\cos\theta(\tau)-v_y(\tau)\sin\theta(\tau)] d\tau$$
• 方法：用 Simpson 公式近似积分 $$\int_a^b f(\xi)d\xi \approx \tfrac{b-a}{6}\,[f(a)+4f(\tfrac{a+b}{2})+f(b)]$$
• 目的：在轨迹优化中高效、可微地计算积分值。
• 特点：数值计算近似，不是模型近似；误差阶次 $O(h^4)$。

(4) 总结

• iLQR/MPC 的线性化 → 针对动力学模型，是“模型近似”，核心目的是 让优化问题可解。
• Simpson 积分 → 针对积分运算，是“计算近似”，核心目的是 让积分算得快而准。

Q3.前进切换到后退的换挡点，需要依赖初始解吗？

这个特性感觉有点厉害了，类似这种换挡的轨迹，不知道需不需要要依赖初始解，如果它能够自动找到最优换挡点，那就太厉害了。 MS 轨迹具有显著优势，它能够避免由于非完整约束动力学所引起的奇异性。这意味着，一条统一的轨迹就可以同时包含前进和后退两种运动，而不需要由前端规划器显式指定。 换挡点是优化的自由度，优化器会在代价函数（安全性、平滑性、能耗等）和约束条件（动力学、障碍物）下，自动决定最优的切换时机和位置。 这个问题的答案需要在代码里进行确认，之后公布。

Q4.轨迹优化中目标函数都有哪些构成

(A) 最终目标：PHR-ALM 形式

(B) 惩罚基底目标 $J'_s$

(C) 平滑度 + 时间正则 $J_0$

(D) 不等式约束惩罚项 $I_d$

采样点约束函数：

(E) 终点位置残差 $C_{f\iota}$

(F) 末端位置积分（辛普森法）

被积函数：

(G) 多项式系数 (c) 的线性关系

因此 $c=c(w_{\sigma'},\,T,\,s_f)$。

(H) 时间正性（平滑双射）

(I) 末端弧长 $s_f$ 的梯度传导

(J) 总览：所有子项回收至最终式

(1) 第一大块：$J'_s$

• $J_0$： 表示轨迹的 平滑度代价（高阶导数的加权积分） + 时间代价。
• $\sum I_d$： 表示所有 不等式约束（速度、加速度、安全距离、分段时长平衡）在采样点上计算的 惩罚函数项。
• 因此，$J'_s$ 是“平滑 + 时间 + 不等式约束惩罚”的 惩罚基底目标。

(2) 第二大块：ALM 增广项